How do you find the period of a trigonometric function?

The period of a trigonometric function is closely related to the frequency of the function. They are related but not the exact same thing.

Period vs Frequency: The difference between the period and the frequency of a trigonometric function is that the frequency is how fast a period is happening and a period defines how often a period happens.

$$f(s+p)=f(s)$$

For the smallest value of s, is what defines a set period of the function given.

Let's take a look at a simple sin(x) graph between $-\pi$ and $\pi$.

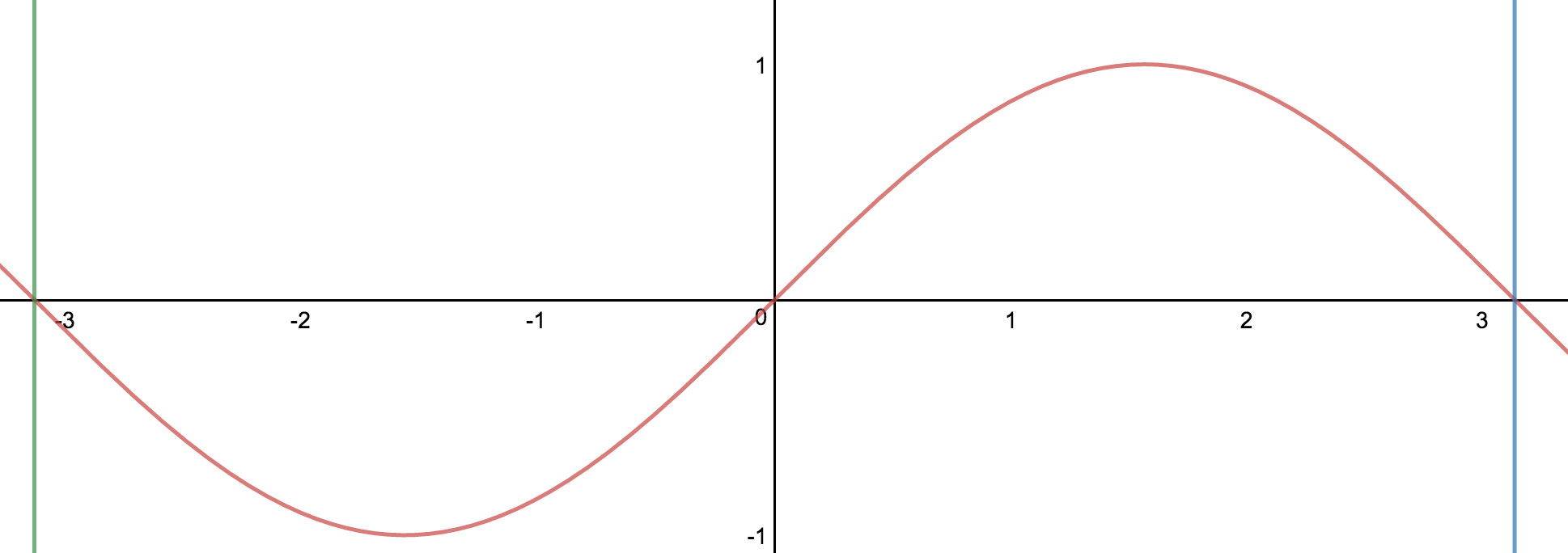
You can take the same graph from a different perspective let's say from $0$ to $2\pi$.

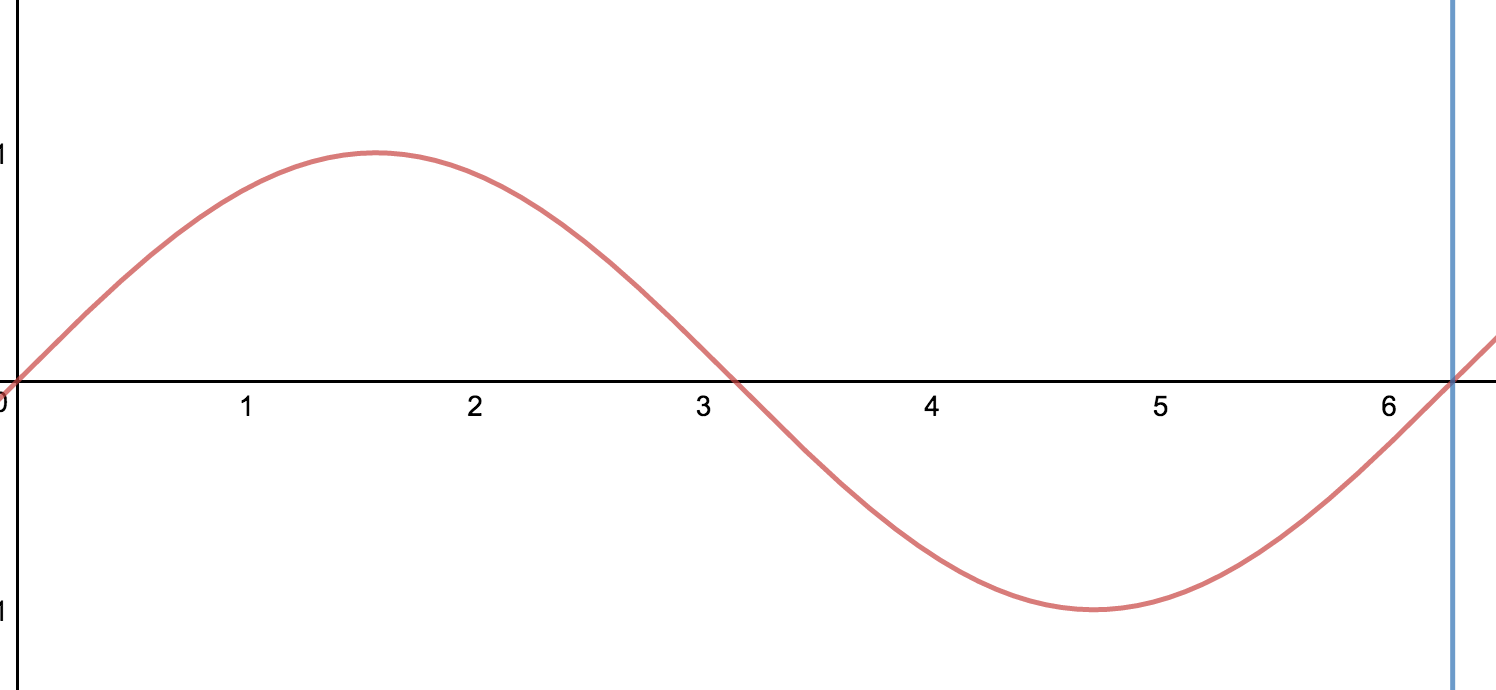
As you can see it's the same graph. You can now define that this graph requires a full $2\pi$ length to complete a full period.

$$0\ to\ \frac { 2\pi}{ b } $$ where b is always the absolute value.

Let's stretch the wave with a smaller frequency. For example 1/2.

$$sin(\frac{1}{2}x)$$

The graph would look like this.

If you work through the algebra.

$$y=Asin(Bx-C)+D$$

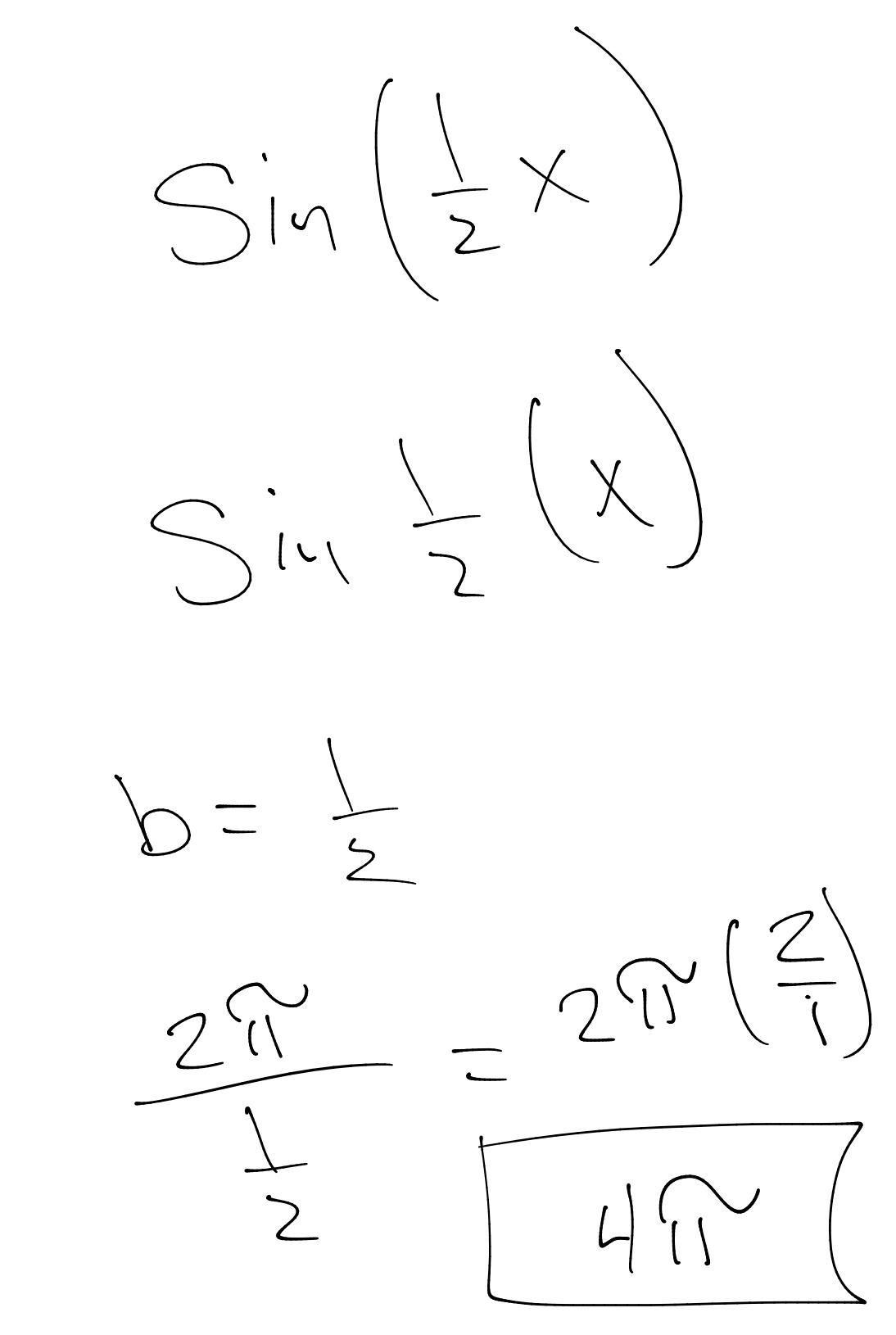
You will end up with a period of $4\pi$ and a frequency of $\frac {1}{2}$

Just to compare with a basic sin wave.

The red and black line defines a complete period for the graph of $sin(\frac{1}{2}x)$ and the purple and blue line define the period for just the standard $sin(x)$ function.