How do you find the frequency of a trigonometric function?

The frequency is closely related to the period of the base trigonometric functions. Since we are using the definition of the length of the given circle to be 1 the frequency of the base functions is $2\pi$.

This means for the base function to complete a full revolution around the circle it's going to take $2\pi$ length. Below you will see the base function of $sin(x)$ with the length of $2\pi$.

$$sin(x)$$

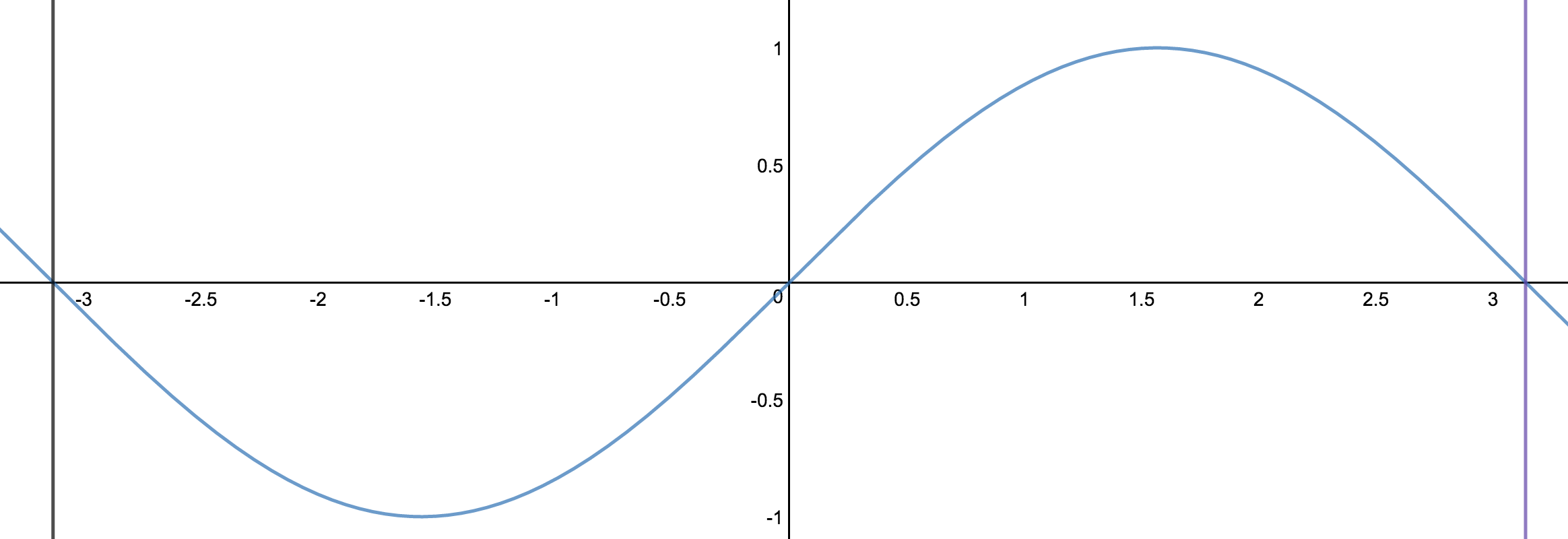
The purple and black lines are $\pi$ length away from the origin and if you add up the values of both distances from the origin you will end up with $2\pi$ length.

If you continue with compressing the function based on the base function by a factor of 2 you will go twice as fast around the circle causing a compression in the $2\pi$ length.

$$sin(2x)$$

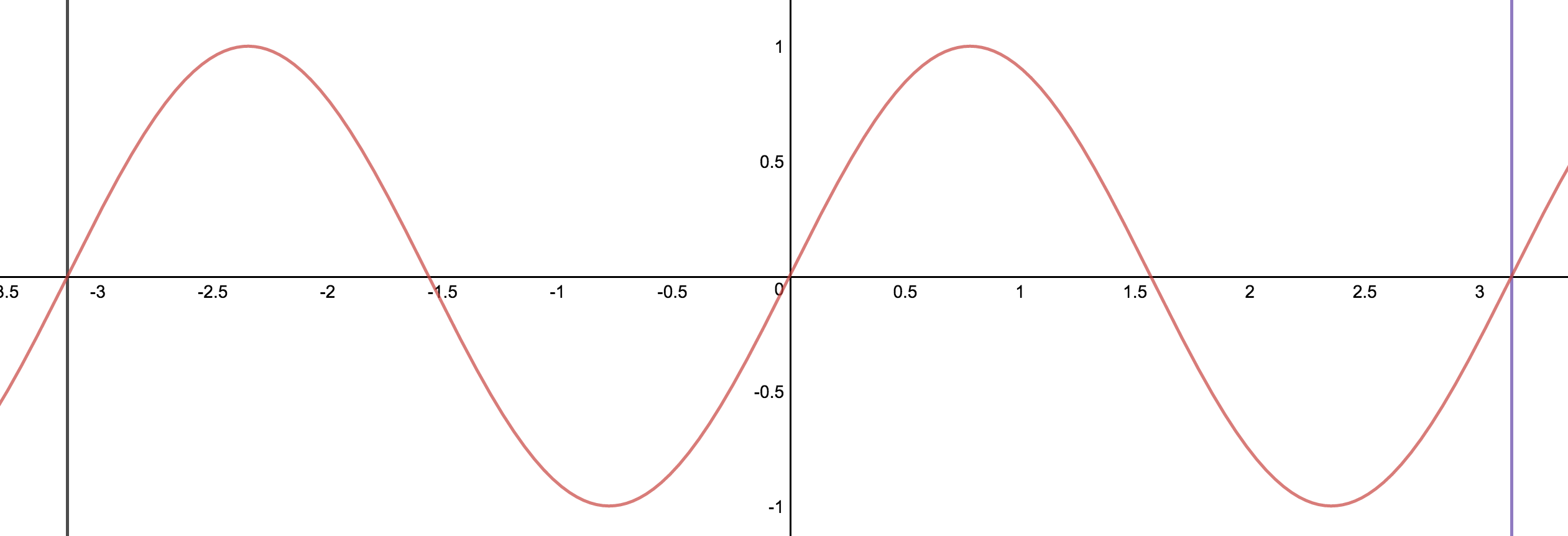
Same would apply for the stretching of the function. If you want to stretch the function you will have to multiply by a value that is less than one. In the example below, you can see that the function is getting delayed by half causing the function to be stretched in the $2\pi$ length.

$$sin(\frac{1}{2}x)$$

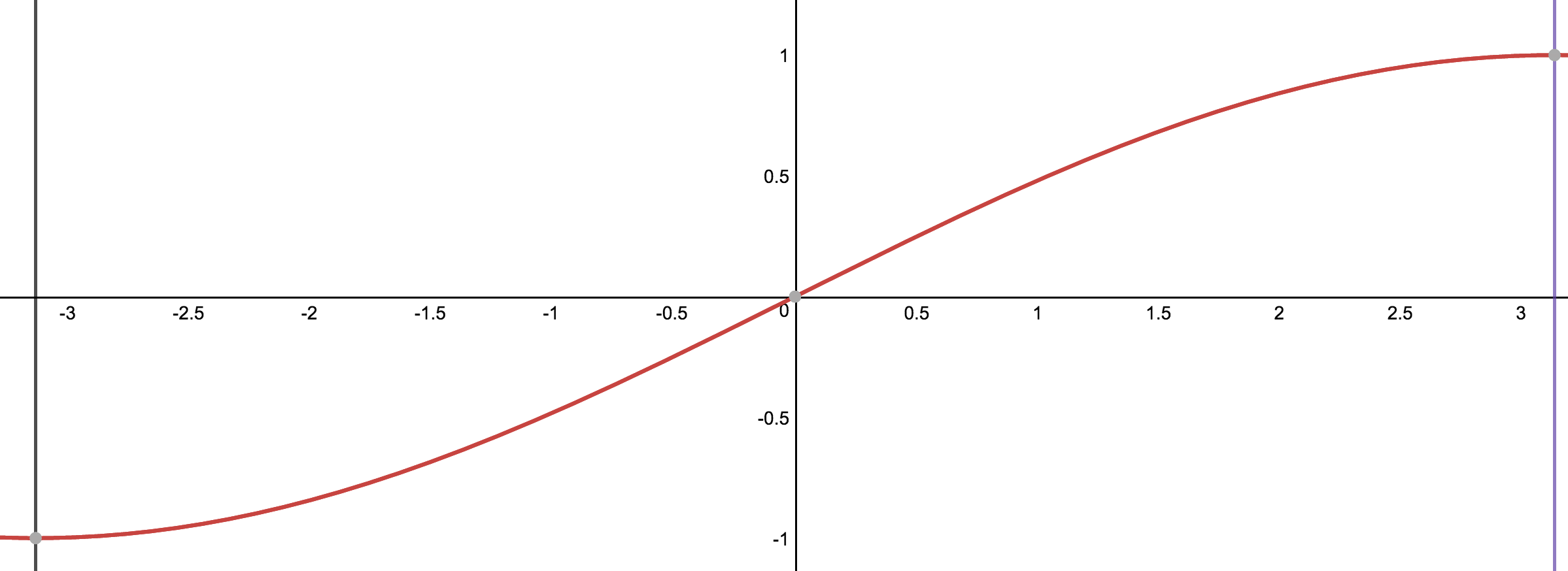
Now to wrap it all up let's see all three functions put together in the $2\pi$ length from the origin.

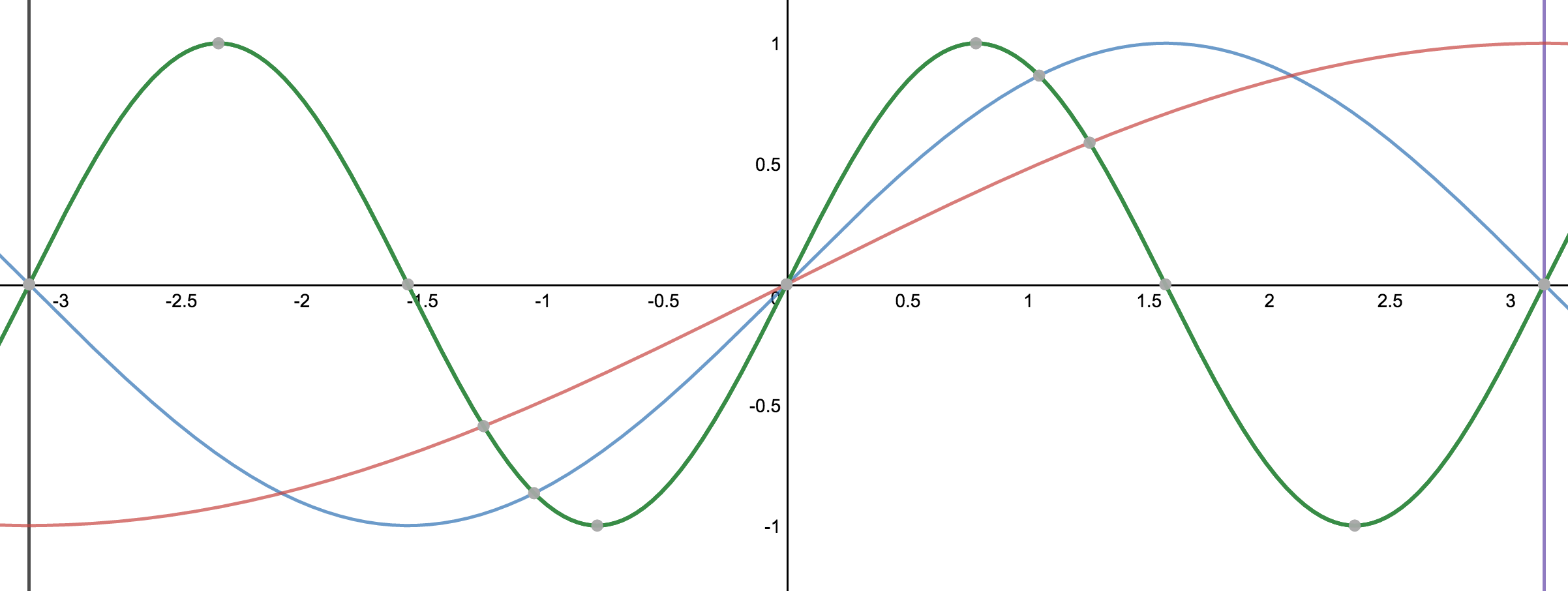
If you look at the graph it should make perfect sense.

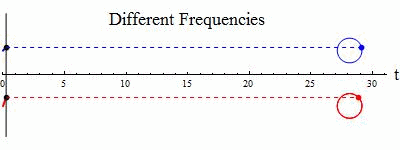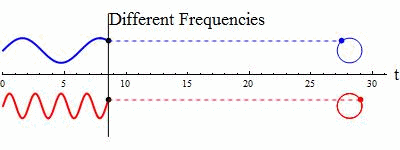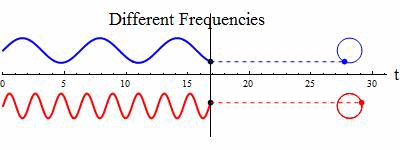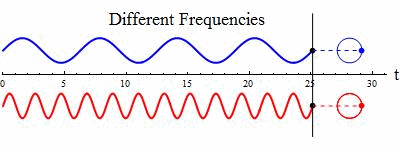
Just for fun and giggles keep this image in mind when you are thinking of frequency.