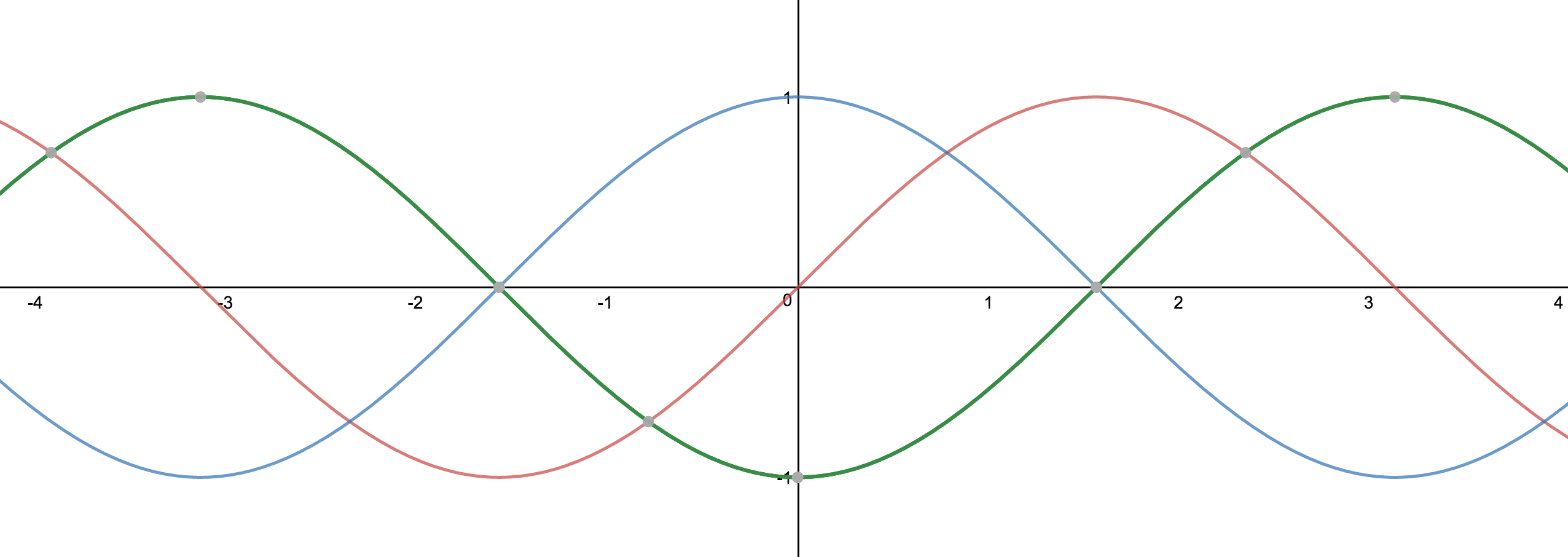
How do you find the phase shift of a trigonometric function?

The phase shift of a graph determines if the graph is going to be shifted left or right on the x-plane of the graph.

$$Asin[B(x-\frac{C}{B})]+D$$

From the example above the phase shift of the graph would be.

$$\frac{C}{B}$$

Let's do a short example of how the phase shifts would happen to a basic sin(x) function.

$$sin(x)$$

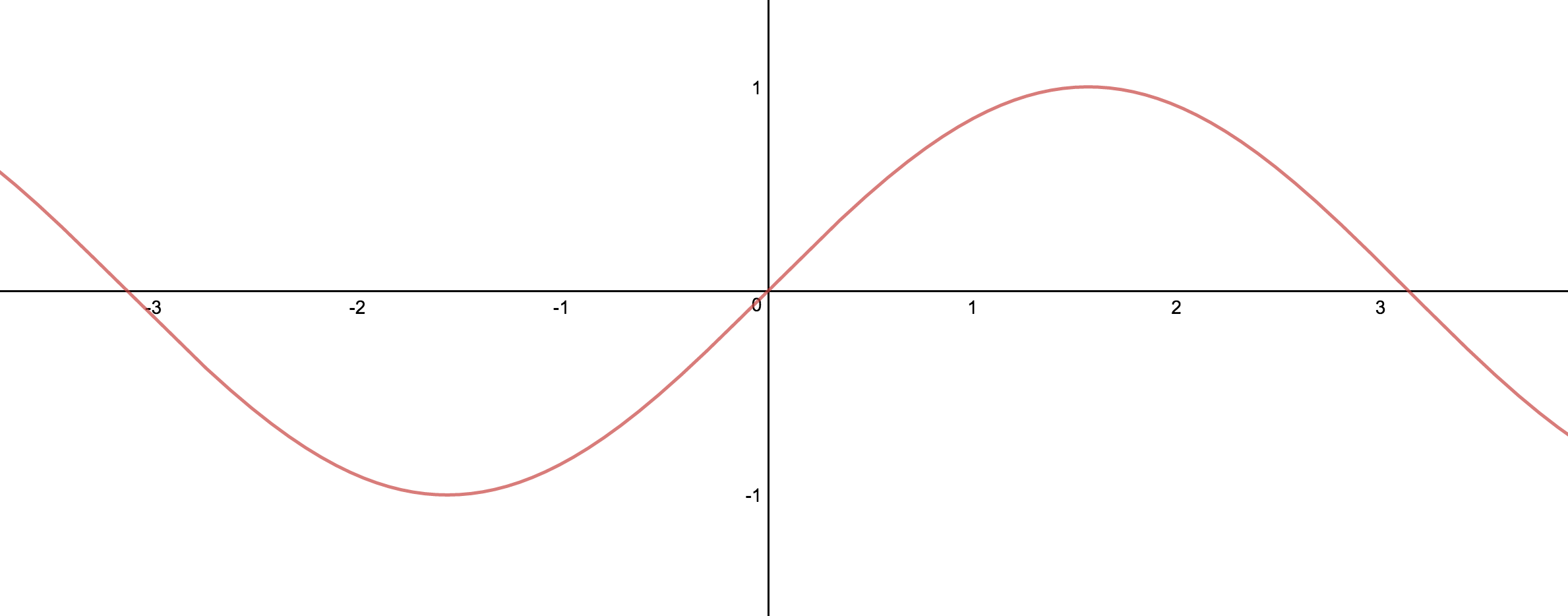
If you take the function and shift it to the left $\frac{\pi}{2}$ length.

$$sin(x+\frac{\pi}{2})$$

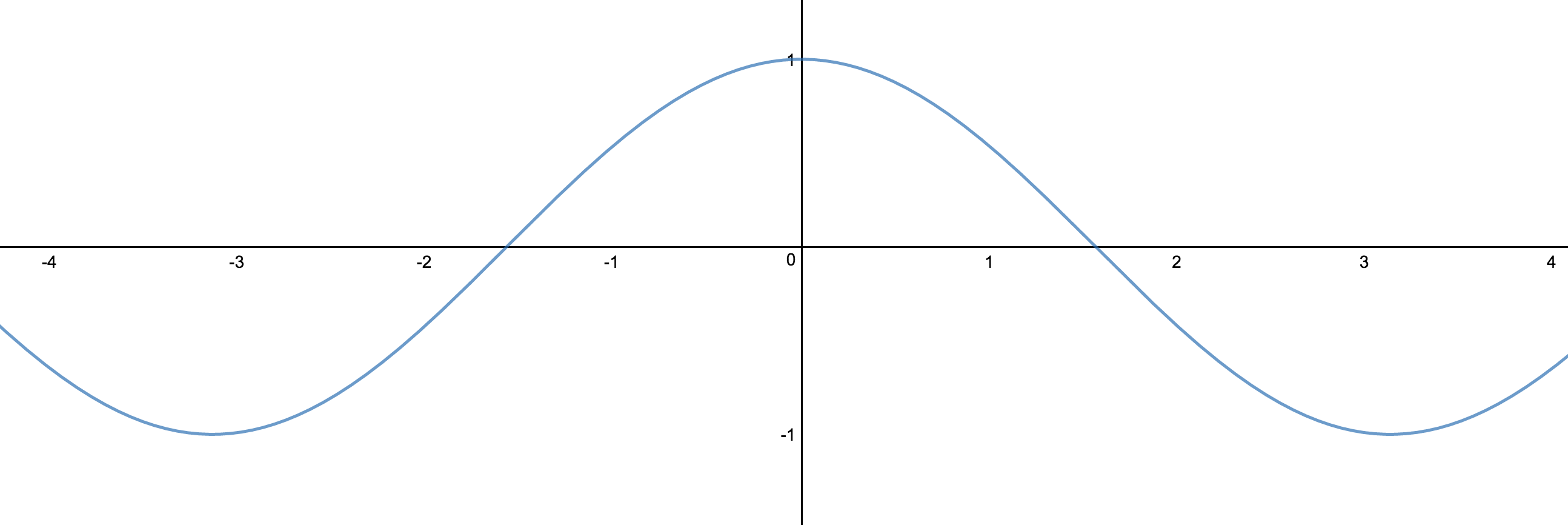
You can also go the other way and shift it to the right $\frac{\pi}{2}$ length.

$$sin(x-\frac{\pi}{2})$$

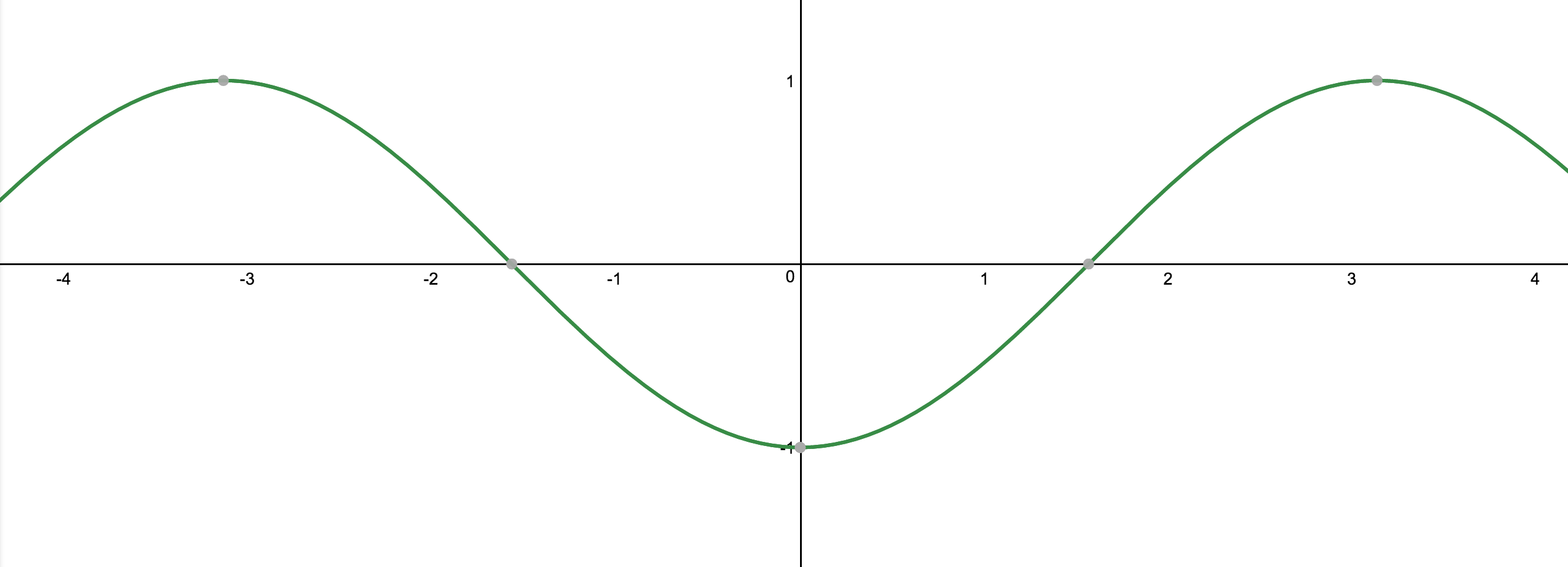
Let's take a look at all three transformations.