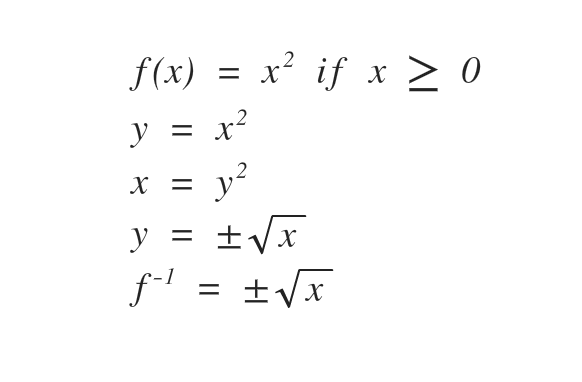How to find the inverse function of a one to one function?

If we truly have a one to one function then only one value for x matches one value for y, so then y has only one value for x.

We can denote an inverse of a function with

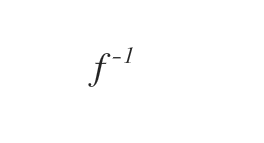
Hold on how do we find the inverse of a set, it's easy all you have to do is switch all the values of x for y and all the values of y for x. Sound familiar? it comes right of the definition.

Now that we understand the inverse of a set we can understand how to find the inverse of a function.

• Step 1: Interchange f(x) with y
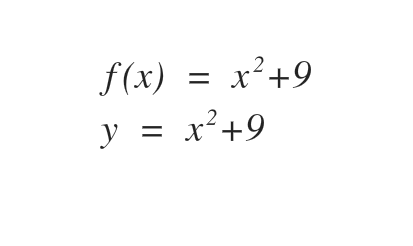
• Step 2: Interchange x and y
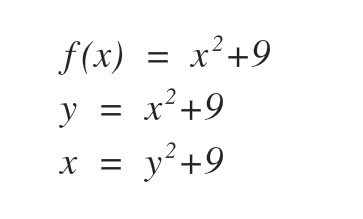
• Step 3: solve for y (explicit form) and covert to inverse function notation
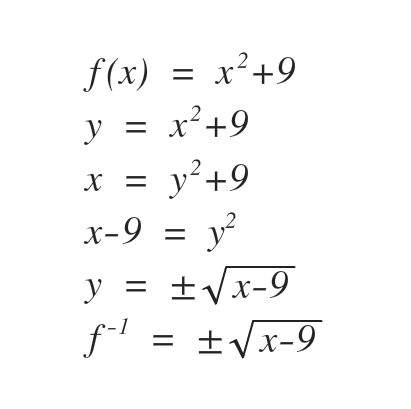
• Step 4: Confirm that the function is one to one with the following

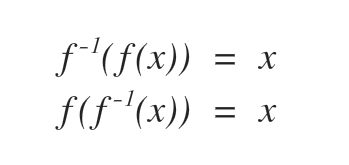
What about functions with domain restrictions? Good question, remember if the graph is always increasing or decreasing then it's a one to one function and the domain restrictions can make that happen.

Example