How to Identify symmetry with respect to the x-axis, y-axis, and the origin of an equation.

To test for symmetry we have to check three parts for symmetry x-axis, y-axis, and the origin.

• x-Axis replace y by 􏰁-y in the equation and simplify. If an equivalent equation is the result then it has x-axis symmetry.
• y-Axis replace x by 􏰁-x in the equation and simplify. If an equivalent equation is the result then it has y-axis symmetry.
• Origin replace x by 􏰁x and -y by 􏰁-y in the equation and simplify. If an equivalent equation is the result then it has x-axis, y-axis and origin symmetry.

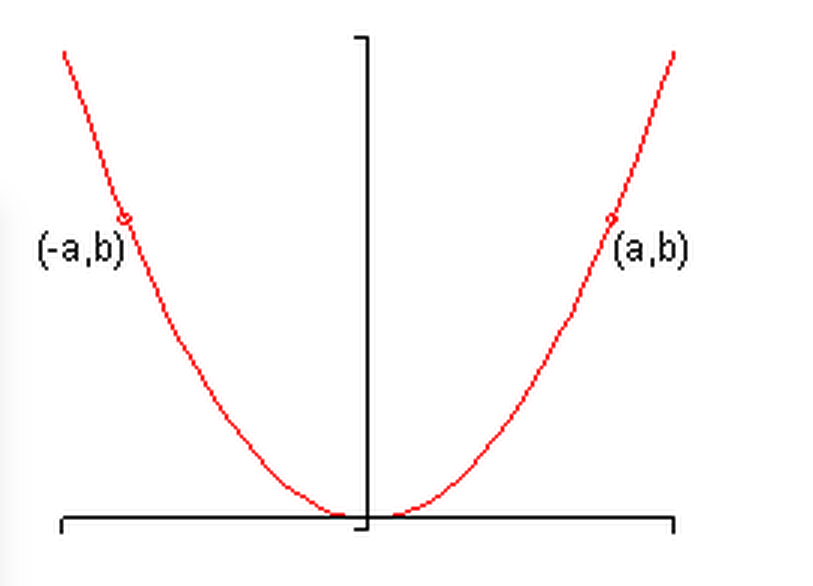
Example of x-Axis ${(x,y) \rightarrow (x,-y) }$
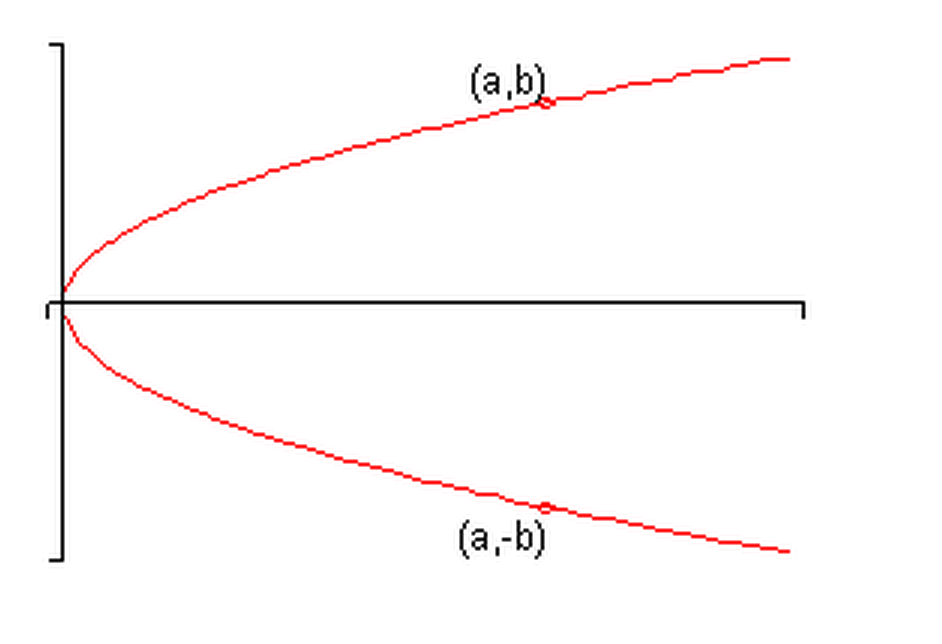Example of y-Axis ${(-x,y) \rightarrow (x,y)}$
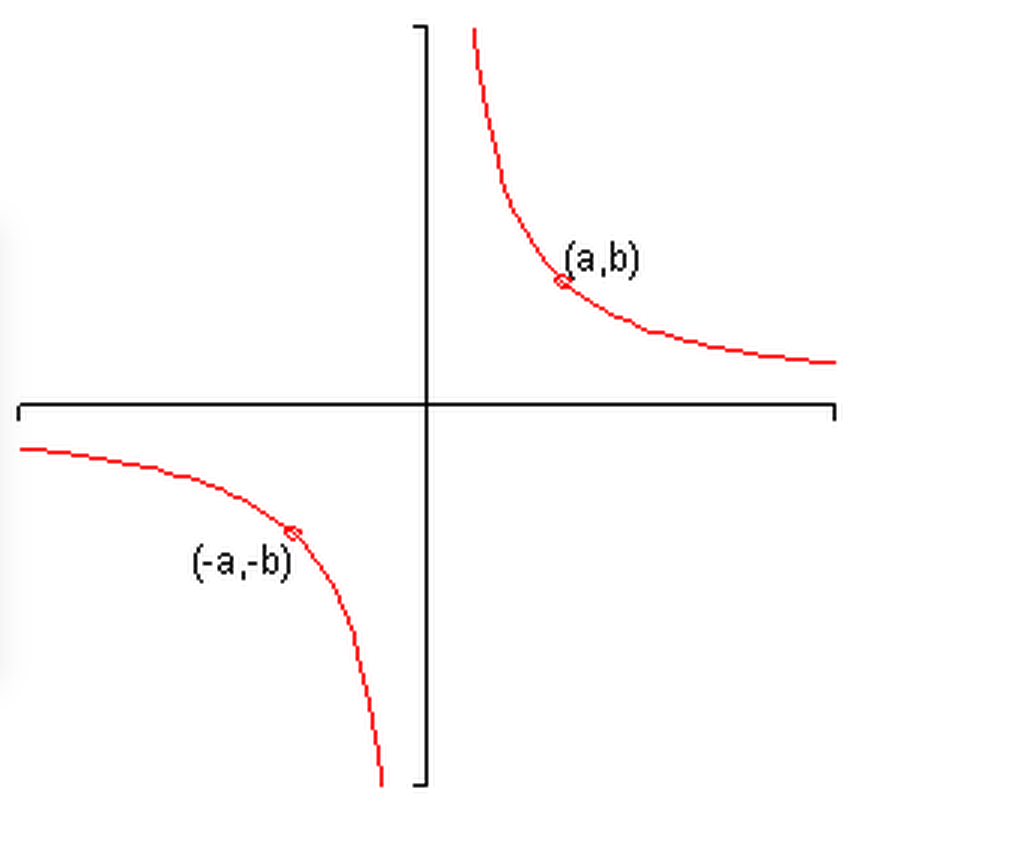
Example of origin symmetry ${(x,y) \rightarrow (-x,-y)}$